Crear una Red Neuronal en Python desde cero

26/07/201815/07/2020 Na8

Programaremos una red neuronal artificial en Python, sin utilizar librerías de terceros. Entrenaremos el modelo y en pocas lineas el algoritmo podrá conducir por sí mismo un coche robot!.

Para ello, explicaremos brevemente la arquitectura de la red neuronal, explicaremos el concepto Forward Propagation y a continuación el de Backpropagation donde ocurre “la magia” y [icon name=”angle-double-left” class=”” unprefixed_class=””]aprenden las neuronas[icon name=”angle-double-right” class=”” unprefixed_class=””].

Asumimos que se tienen conocimientos básicos de Redes Neuronales y de Python, les recomiendo repasar algunos conceptos en los artículos:

Comencemos con un Ejercicio Práctico

Este amigable coche robot Arduino, será a quien le implantaremos nuestra red neuronal, para que pueda conducir sólo, evitando los obstáculos!

Vamos a crear una red neuronal que conduzca un coche de juguete Arduino que más adelante construiremos y veremos en el “mundo real”.

Nuestros datos de entrada serán:

Sensor de distancia al obstáculo
- si es 0 no hay obstáculos a la vista
- si es 0,5 se acerca a un obstáculo
- si es 1 está demasiado cerca de un obstáculo
Posición del obstáculo (izquierda,derecha)
- El obstáculo es visto a la izquierda será -1
- visto a la derecha será 1

Las salidas serán

Girar
- derecha 1 / izquierda -1
Dirección
- avanzar 1 / retroceder -1

La velocidad del vehículo podría ser una salida más (por ejemplo disminuir la velocidad si nos aproximamos a un objeto) y podríamos usar más sensores como entradas pero por simplificar el modelo y su implementación mantendremos estas 2 entradas y 2 salidas.

Para entrenar la red tendremos las entradas y salidas que se ven en la tabla:

Entrada: Sensor Distancia	Entrada: Posición Obstáculo	Salida: Giro	Salida: Dirección	Acción de la Salida
0	0	0	1	Avanzar
0	1	0	1	Avanzar
0	-1	0	1	Avanzar
0.5	1	-1	1	Giro a la izquierda
0.5	-1	1	1	Giro a la derecha
0.5	0	0	1	Avanzar
1	1	0	-1	Retroceder
1	-1	0	-1	Retroceder
1	0	0	-1	Retroceder
-1	0	0	1	Avanzar
-1	-1	0	1	Avanzar
-1	1	0	1	Avanzar

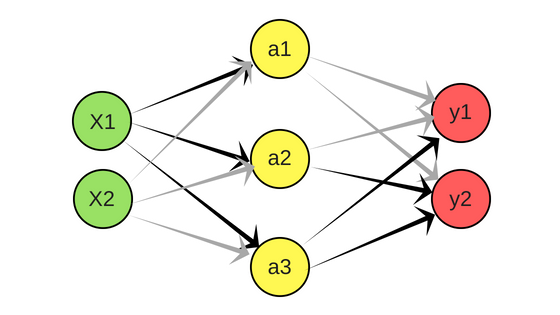
Esta será la arquitectura de la red neuronal propuesta:

En la imagen anterior -y durante el ejemplo- usamos la siguiente notación en las neuronas:

X(i) son las entradas
a(i) activación en la capa 2
y(i) son las salidas

Y quedan implícitos, pero sin representación en la gráfica:

O(j) Los pesos de las conexiones entre neuronas será una matriz que mapea la capa j a la j+1
Recordemos que utilizamos 1 neurona extra en la capa 1 y una neurona extra en la capa 2 a modo de Bias -no están en la gráfica- para mejorar la precisión de la red neuronal, dandole mayor “libertad algebraica”.

Los cálculos para obtener los valores de activación serán:

a(1) = g(O^T₁X)

a(2) = g(O^T₂X)

a(3) = g(O^T₃X)

*Nota: la T indica matriz traspuesta, para poder hacer el producto

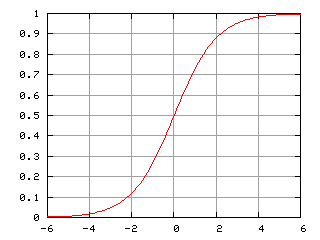
En las ecuaciones, la g es una función Sigmoide que refiere al caso especial de función logística y definida por la fórmula:

g(z) = 1/(1+e^-z)

Funciones Sigmoide

Una de las razones para utilizar la función sigmoide –función Logística– es por sus propiedades matemáticas, en nuestro caso, sus derivadas. Cuando más adelante la red neuronal haga backpropagation para aprender y actualizar los pesos, haremos uso de su derivada. En esta función puede ser expresada como productos de f y 1-f . Entonces f'(t) = f(t)(1 – f(t)). Por ejemplo la función tangente y su derivada arco-tangente se utilizan normalizadas, donde su pendiente en el origen es 1 y cumplen las propiedades.

Imagen de la Curva Logística Normalizada de Wikipedia

Forward Propagation -ó red Feedforward-

Con Feedforward nos referimos al recorrido de “izquierda a derecha” que hace el algoritmo de la red, para calcular el valor de activación de las neuronas desde las entradas hasta obtener los valores de salida.

Si usamos notación matricial, las ecuaciones para obtener las salidas de la red serán:

X = [x₀x₁x₂]

z^layer2 = O₁X

a^layer2 = g(z^layer2)

z^layer3 = O₂a^layer2

y = g(z^layer3)

Resumiendo: tenemos una red; tenemos 2 entradas, éstas se multiplican por los pesos de las conexiones y cada neurona en la capa oculta suma esos productos y les aplica la función de activación para “emitir” un resultado a la siguiente conexión (concepto conocido en biología como sinapsis química).

Como bien sabemos, los pesos iniciales se asignan con valores entre -1 y 1 de manera aleatoria. El desafío de este algoritmo, será que las neuronas aprendan por sí mismas a ajustar el valor de los pesos para obtener las salidas correctas.

Backpropagation (cómputo del gradiente)

Al hacer backpropagtion es donde el algoritmo itera para aprender! Esta vez iremos de “derecha a izquierda” en la red para mejorar la precisión de las predicciones. El algoritmo de backpropagation se divide en dos Fases: Propagar y Actualizar Pesos.

Fase 1: Propagar

Esta fase implica 2 pasos:

1.1 Hacer forward propagation de un patrón de entrenamiento (recordemos que es este es un algoritmo supervisado, y conocemos las salidas) para generar las activaciones de salida de la red.

1.2 Hacer backward propagation de las salidas (activación obtenida) por la red neuronal usando las salidas “y” reales para generar los Deltas (error) de todas las neuronas de salida y de las neuronas de la capa oculta.

Fase 2: Actualizar Pesos:

Para cada <<sinapsis>> de los pesos:

2.1 Multiplicar su delta de salida por su activación de entrada para obtener el gradiente del peso.

2.2 Substraer un porcentaje del gradiente de ese peso

El porcentaje que utilizaremos en el paso 2.2 tiene gran influencia en la velocidad y calidad del aprendizaje del algoritmo y es llamado “learning rate” ó tasa de aprendizaje. Si es una tasa muy grande, el algoritmo aprende más rápido pero tendremos mayor imprecisión en el resultado. Si es demasiado pequeño, tardará mucho y podría no finalizar nunca.

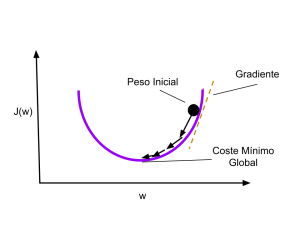
En esta gráfica vemos cómo utilizamos el gradiente paso a paso para descender y minimizar el coste total. Cada paso utilizará la Tasa de Aprendizaje -learning rate- que afectará la velocidad y calidad de la red.

Deberemos repetir las fases 1 y 2 hasta que la performance de la red neuronal sea satisfactoria.

Si denotamos al error en el layer “l” como d(l) para nuestras neuronas de salida en layer 3 la activación menos el valor actual será (usamos la forma vectorial):

d(3) = a^layer3 – y

d(2) = O^T₂ d(3) . g'(z^layer2)

g'(z^layer2) = a^layer2 . (1 – a^layer2)

Al fin aparecieron las derivadas! Nótese que no tendremos delta para la capa 1, puesto que son los valores X de entrada y no tienen error asociado.

El valor del costo -que es lo que queremos minimizar- de nuestra red será

J = a^layer d^{layer + 1}

Usamos este valor y lo multiplicamos al learning rate antes de ajustar los pesos. Esto nos asegura que buscamos el gradiente, iteración a iteración “apuntando” hacia el mínimo global.

self.weights[i] += learning_rate * layer.T.dot(delta)

1	self.weights[i] += learning_rate * layer.T.dot(delta)

Nota: el layer en el código es realmente a(l)

El Código Completo de la red Neuronal con Backpropagation

Aquí va el código, recuerden que lo pueden ver y descargar al final del artículo o desde mi cuenta de GitHub.

Primero, declaramos la clase NeuralNetwork

import numpy as np

def sigmoid(x):
    return 1.0/(1.0 + np.exp(-x))

def sigmoid_derivada(x):
    return sigmoid(x)*(1.0-sigmoid(x))

def tanh(x):
    return np.tanh(x)

def tanh_derivada(x):
    return 1.0 - x**2


class NeuralNetwork:

    def __init__(self, layers, activation='tanh'):
        if activation == 'sigmoid':
            self.activation = sigmoid
            self.activation_prime = sigmoid_derivada
        elif activation == 'tanh':
            self.activation = tanh
            self.activation_prime = tanh_derivada

        # inicializo los pesos
        self.weights = []
        self.deltas = []
        # capas = [2,3,2]
        # rando de pesos varia entre (-1,1)
        # asigno valores aleatorios a capa de entrada y capa oculta
        for i in range(1, len(layers) - 1):
            r = 2*np.random.random((layers[i-1] + 1, layers[i] + 1)) -1
            self.weights.append(r)
        # asigno aleatorios a capa de salida
        r = 2*np.random.random( (layers[i] + 1, layers[i+1])) - 1
        self.weights.append(r)

    def fit(self, X, y, learning_rate=0.2, epochs=100000):
        # Agrego columna de unos a las entradas X
        # Con esto agregamos la unidad de Bias a la capa de entrada
        ones = np.atleast_2d(np.ones(X.shape[0]))
        X = np.concatenate((ones.T, X), axis=1)
        
        for k in range(epochs):
            i = np.random.randint(X.shape[0])
            a = [X[i]]

            for l in range(len(self.weights)):
                    dot_value = np.dot(a[l], self.weights[l])
                    activation = self.activation(dot_value)
                    a.append(activation)
            # Calculo la diferencia en la capa de salida y el valor obtenido
            error = y[i] - a[-1]
            deltas = [error * self.activation_prime(a[-1])]
            
            # Empezamos en el segundo layer hasta el ultimo
            # (Una capa anterior a la de salida)
            for l in range(len(a) - 2, 0, -1): 
                deltas.append(deltas[-1].dot(self.weights[l].T)*self.activation_prime(a[l]))
            self.deltas.append(deltas)

            # invertir
            # [level3(output)->level2(hidden)]  => [level2(hidden)->level3(output)]
            deltas.reverse()

            # backpropagation
            # 1. Multiplcar los delta de salida con las activaciones de entrada 
            #    para obtener el gradiente del peso.
            # 2. actualizo el peso restandole un porcentaje del gradiente
            for i in range(len(self.weights)):
                layer = np.atleast_2d(a[i])
                delta = np.atleast_2d(deltas[i])
                self.weights[i] += learning_rate * layer.T.dot(delta)

            if k % 10000 == 0: print('epochs:', k)

    def predict(self, x): 
        ones = np.atleast_2d(np.ones(x.shape[0]))
        a = np.concatenate((np.ones(1).T, np.array(x)), axis=0)
        for l in range(0, len(self.weights)):
            a = self.activation(np.dot(a, self.weights[l]))
        return a

    def print_weights(self):
        print("LISTADO PESOS DE CONEXIONES")
        for i in range(len(self.weights)):
            print(self.weights[i])

    def get_deltas(self):
        return self.deltas

import numpy as np

def sigmoid(x):

return 1.0/(1.0 + np.exp(-x))

def sigmoid_derivada(x):

return sigmoid(x)*(1.0-sigmoid(x))

def tanh(x):

return np.tanh(x)

def tanh_derivada(x):

return 1.0 - x**2

class NeuralNetwork:

def __init__(self, layers, activation='tanh'):

if activation == 'sigmoid':

self.activation = sigmoid

self.activation_prime = sigmoid_derivada

elif activation == 'tanh':

self.activation = tanh

self.activation_prime = tanh_derivada

# inicializo los pesos

self.weights = []

self.deltas = []

# capas = [2,3,2]

# rando de pesos varia entre (-1,1)

# asigno valores aleatorios a capa de entrada y capa oculta

for i in range(1, len(layers) - 1):

r = 2*np.random.random((layers[i-1] + 1, layers[i] + 1)) -1

self.weights.append(r)

# asigno aleatorios a capa de salida

r = 2*np.random.random( (layers[i] + 1, layers[i+1])) - 1

self.weights.append(r)

def fit(self, X, y, learning_rate=0.2, epochs=100000):

# Agrego columna de unos a las entradas X

# Con esto agregamos la unidad de Bias a la capa de entrada

ones = np.atleast_2d(np.ones(X.shape[0]))

X = np.concatenate((ones.T, X), axis=1)

for k in range(epochs):

i = np.random.randint(X.shape[0])

a = [X[i]]

for l in range(len(self.weights)):

dot_value = np.dot(a[l], self.weights[l])

activation = self.activation(dot_value)

a.append(activation)

# Calculo la diferencia en la capa de salida y el valor obtenido

error = y[i] - a[-1]

deltas = [error * self.activation_prime(a[-1])]

# Empezamos en el segundo layer hasta el ultimo

# (Una capa anterior a la de salida)

for l in range(len(a) - 2, 0, -1):

deltas.append(deltas[-1].dot(self.weights[l].T)*self.activation_prime(a[l]))

self.deltas.append(deltas)

# invertir

# [level3(output)->level2(hidden)] => [level2(hidden)->level3(output)]

deltas.reverse()

# backpropagation

# 1. Multiplcar los delta de salida con las activaciones de entrada

# para obtener el gradiente del peso.

# 2. actualizo el peso restandole un porcentaje del gradiente

for i in range(len(self.weights)):

layer = np.atleast_2d(a[i])

delta = np.atleast_2d(deltas[i])

self.weights[i] += learning_rate * layer.T.dot(delta)

if k % 10000 == 0: print('epochs:', k)

def predict(self, x):

ones = np.atleast_2d(np.ones(x.shape[0]))

a = np.concatenate((np.ones(1).T, np.array(x)), axis=0)

for l in range(0, len(self.weights)):

a = self.activation(np.dot(a, self.weights[l]))

return a

def print_weights(self):

print("LISTADO PESOS DE CONEXIONES")

for i in range(len(self.weights)):

print(self.weights[i])

def get_deltas(self):

return self.deltas

Y ahora creamos una red a nuestra medida, con 2 neuronas de entrada, 3 ocultas y 2 de salida. Deberemos ir ajustando los parámetros de entrenamiento learning rate y la cantidad de iteraciones “epochs” para obtener buenas predicciones.

# funcion Coche Evita obstáculos
nn = NeuralNetwork([2,3,2],activation ='tanh')
X = np.array([[0, 0],   # sin obstaculos
              [0, 1],   # sin obstaculos
              [0, -1],  # sin obstaculos
              [0.5, 1], # obstaculo detectado a derecha
              [0.5,-1], # obstaculo a izq
              [1,1],    # demasiado cerca a derecha
              [1,-1]])  # demasiado cerca a izq

y = np.array([[0,1],    # avanzar
              [0,1],    # avanzar
              [0,1],    # avanzar
              [-1,1],   # giro izquierda
              [1,1],    # giro derecha
              [0,-1],   # retroceder
              [0,-1]])  # retroceder
nn.fit(X, y, learning_rate=0.03,epochs=15001)

index=0
for e in X:
    print("X:",e,"y:",y[index],"Network:",nn.predict(e))
    index=index+1

# funcion Coche Evita obstáculos

nn = NeuralNetwork([2,3,2],activation ='tanh')

X = np.array([[0, 0], # sin obstaculos

[0, 1], # sin obstaculos

[0, -1], # sin obstaculos

[0.5, 1], # obstaculo detectado a derecha

[0.5,-1], # obstaculo a izq

[1,1], # demasiado cerca a derecha

[1,-1]]) # demasiado cerca a izq

y = np.array([[0,1], # avanzar

[0,1], # avanzar

[-1,1], # giro izquierda

[1,1], # giro derecha

[0,-1], # retroceder

[0,-1]]) # retroceder

nn.fit(X, y, learning_rate=0.03,epochs=15001)

index=0

for e in X:

print("X:",e,"y:",y[index],"Network:",nn.predict(e))

index=index+1

La salidas obtenidas son: (comparar los valores “y” con los de “Network” )

X: [0. 0.]     y: [0 1]   Network: [0.00112476   0.99987346]
X: [0. 1.]     y: [0 1]   Network: [-0.00936178  0.999714  ]
X: [ 0. -1.]   y: [0 1]   Network: [0.00814966   0.99977055]
X: [0.5 1. ]   y: [-1  1] Network: [-0.92739127  0.96317035]
X: [ 0.5 -1. ] y: [1 1]   Network: [0.91719235   0.94992698]
X: [1. 1.]     y: [ 0 -1] Network: [-8.81827252e-04 -9.79524215e-01]
X: [ 1. -1.]   y: [ 0 -1] Network: [ 0.00806883  -0.96823086]

X: [0. 0.] y: [0 1] Network: [0.00112476 0.99987346]

X: [0. 1.] y: [0 1] Network: [-0.00936178 0.999714 ]

X: [ 0. -1.] y: [0 1] Network: [0.00814966 0.99977055]

X: [0.5 1. ] y: [-1 1] Network: [-0.92739127 0.96317035]

X: [ 0.5 -1. ] y: [1 1] Network: [0.91719235 0.94992698]

X: [1. 1.] y: [ 0 -1] Network: [-8.81827252e-04 -9.79524215e-01]

X: [ 1. -1.] y: [ 0 -1] Network: [ 0.00806883 -0.96823086]

Como podemos ver son muy buenos resultados.

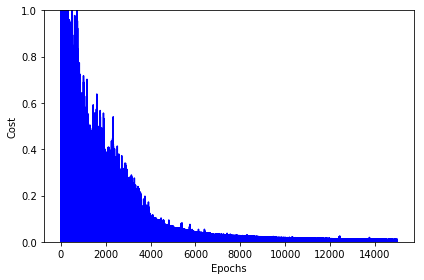
Aquí podemos ver como el coste de la función se va reduciendo y tiende a cero:

import matplotlib.pyplot as plt

deltas = nn.get_deltas()
valores=[]
index=0
for arreglo in deltas:
    valores.append(arreglo[1][0] + arreglo[1][1])
    index=index+1

plt.plot(range(len(valores)), valores, color='b')
plt.ylim([0, 1])
plt.ylabel('Cost')
plt.xlabel('Epochs')
plt.tight_layout()
plt.show()

import matplotlib.pyplot as plt

deltas = nn.get_deltas()

valores=[]

index=0

for arreglo in deltas:

valores.append(arreglo[1][0] + arreglo[1][1])

index=index+1

plt.plot(range(len(valores)), valores, color='b')

plt.ylim([0, 1])

plt.ylabel('Cost')

plt.xlabel('Epochs')

plt.tight_layout()

plt.show()

Y podemos ver los pesos obtenidos de las conexiones con nn.print_weights() pues estos valores serán los que usaremos en la red final que en un próximo artículo implementaremos en Arduino para que un coche-robot conduzca sólo evitando obstáculos.

Conclusión

Creamos una red neuronal en pocas líneas de código Python:

comprendimos cómo funciona una red neuronal “básica”,
el porqué de las funciones Sigmoides y sus derivadas que …
nos permiten hacer Backpropagation,
hallar el gradiente para minimizar el coste,
reducir el error iterando y obtener las salidas buscadas,
logrando que la red aprenda por sí misma en base a un conjunto de datos de entrada y sus salidas como “buen” Algoritmo Supervisado que es.

Nos queda como proyecto futuro aplicar esta red que construimos en el mundo real y comprobar si un coche Arduino será capaz de conducir por sí mismo y evitar obstáculos..! (en el próximo artículo lo veremos en acción!)

Suscripción al Blog

Como siempre, te invito a suscribirte al Blog y recibir los artículos cada 15 días.

Puedes hacer más ejercicios Machine Learning en Python en nuestra categoría d Ejercicios paso a paso por ejemplo de Regresión Logística ó clustering K-means ó comprender y crear una Sencilla Red Neuronal

Recursos

Si tienes que armar tu ambiente de Programación Python puedes hacerlo siguiendo los pasos de este artículo: Instalar ambiente de Desarrollo Python con Anaconda

El código utilizado es una adaptación del original del BogoToBogo en donde se enseña la función XOR.

Pueden descargar el código de este artículo en un Jupyter Notebook aquí o visualizar online ó pueden acceder a mi Github.

Puedes ver la continuación de este artículo en donde aplicaremos la red neuronal a un coche arduino! no te lo pierdas!

Lee acerca de la evolución de las redes neuronales desde 1950 hasta la actualidad

El libro del Blog

Este artículo y todos los demás en el libro del blog . Aún está en borrador, pero apreciaré mucho tu colaboracón! Contiene Extras descargables como el “Lego Dataset” utilizado en el artículo de Detección de Objetos.

37 thoughts on “Crear una Red Neuronal en Python desde cero”

befama says:

27/07/2018 at 21:53

Buen, tema. Espero pronto construir el coche arduino. Saludos y gracias por el blog.

Reply
1. Na8 says:
  
  27/07/2018 at 22:22
  
  Gracias por seguir visitando el blog! Espero publicar el siguiente artículo con la red Neuronal funcionando en arduino la semana que viene o máximo 14 días! En casa ya lo tengo funcionando 🙂
  
  Reply
  1. J.C.Vázquez says:
    
    28/11/2019 at 21:31
    
    Hola. Lindo ejemplo. Creo que puede haber un error al calcular la derivada de la tanh.
    def tanh_derivada(x):
    return 1.0 – x2
    Creo que debería ser:
    def tanh_derivada(x):
    return 1.0 – tanh(x)2
    Saludos.
    
    Reply
Anonimo says:

28/07/2018 at 16:13

Enhorabuena amigo, por tan especial blog, con este tema emergente

Reply
Mario González says:

04/09/2018 at 00:37

Pienso que sería mejor utilizar una base de datos de entrenamiento “real” ya que la utilizada consta sólo de 7 datos hechos a mano, para los cuales programar específicamente las instrucciones entrada-salida es muy fácil de hacer, por lo cual se hace innecesario entrenar una red.

De todas formas buen post e idea de difundir el aprendizaje de redes neuronales.

Reply
1. Rafael Guerrero says:
  
  12/09/2018 at 00:10
  
  la red se entrena una sola vez, o cada vez que se prenda el carrito ?
  
  Reply
  1. Na8 says:
    
    12/09/2018 at 12:12
    
    Una vez creada la red en Python y entrenada (1 sola vez), obtenemos los pesos óptimos de las conexiones entre las capas, y estos valores son los que copiamos en el código arduino. Pero esa red, YA está entrenada, es decir, que ya funciona bien y no es necesario seguir entrenando.
    
    Reply
Rafael Guerrero says:

11/09/2018 at 23:41

Saludos,

Excelente ejemplo!

cual fue el determinante para definir solo una capa oculta con 3 neuronas

como defines la cantidad de capas ocultas y el numero de neuronas en las capas ocultas

Reply
1. Na8 says:
  
  12/09/2018 at 12:10
  
  A decir verdad, para este caso fue prueba y error. Existen algunas “reglas a ojo” (en inglés thumb-rule) comparto este enlace donde se comentan varias: Thumb rules to determine number of hidden layers and cells.
  
  Reply
  1. Rafael Guerrero says:
    
    13/09/2018 at 01:51
    
    ooooOOOOOOh!…. excelente, gracias por tu respuesta
    
    si a tu ejemplo agarro y modifico el numero de neuronas (entradas, capas ocultas y salidas)
    
    y paso unos datos de prueba debería funcionar tambien o aproximarse a lo que estoy buscando ?
    
    o depende tambien del tipo de función que tiene cada neurona ?
    
    Reply
    1. Na8 says:
      
      25/09/2018 at 01:24
      
      Si modificas capas y cantidad de neuronas, deberías obtener buenos resultados, siempre y cuando no caigas en Overfitting ó Underfitting. En cuanto a la función, por lo general se utiliza la misma función en una misma capa (por ejemplo ReLu) y en toda la red, o puede que se cambie la función en la capa de entrada y salida (por ejemplo para una salida SoftMax para clasificar resultados mutuamente excluyentes).
      
      Reply
Nagib says:

15/10/2018 at 22:58

hola te comento que el link de github cayo no puedo acceder al código de referencia

Reply
1. Na8 says:
  
  16/10/2018 at 00:20
  
  Hola Nagib, acabo de comprobar y me funcionan correctamente todos los enlaces. Te dejo aquí nuevamente el link al código en Github. Dime si te funciona correctamente por favor. Saludos y gracias por escribir!
  
  Reply
  1. Nagib Vallejos Mamani says:
    
    09/11/2018 at 08:30
    
    Ahora si pude tener el acceso, muchas gracias, sigo tu página semana a semana, segui adelante y exitos.
    
    Reply
    1. Na8 says:
      
      09/11/2018 at 14:06
      
      Me alegro!, gracias a ti! Sigamos adelante
      
      Reply
Alfredo says:

21/04/2019 at 13:46

Ayer descubrí tu blog por casualidad, y he estado leyendo varios de tus artículos. Me gustan porque explicas las cosas y das enlaces de tus explicaciones. Ya me he suscrito a tu blog.
Sigue así, muy buen trabajo.

Reply
Na8 says:

28/04/2019 at 22:50

Hola Alfredo!, un gusto conocerte. Espero que te sigan gustando los próximos artículos!. Saludos!

Reply
Jose Flores Bendezú says:

09/05/2019 at 22:49

Gracias Maestro como siempre tu codigo funciona, y tus explicaciones son a todo dar, gracias a ti estoy aprendiendo este maravilloso mundo del learning, un fuerte abrazo donde te encuentres

Reply
1. Na8 says:
  
  16/05/2019 at 13:22
  
  Hola Jose Flores, muchas gracias por el ánimo! Procuraré seguir escribiendo artículos! Saludos y cualquier cosa me dices!
  
  Reply
Jose Felipe Castellot says:

05/07/2019 at 17:05

Estimado Juan Ignacio, muchas felicidades por tu conocimiento y contribución a la comunidad, éste tema en particular me parece muy interesante, prácticamente se puede resolver casi cualquier problema, esperemos ver más artículos tuyos, por cierto tengo una duda, perdón por mi ignorancia, estoy apenas comenzando a meterme en el tema, veo que la función de la derivada de la tangente hiperbólica es 1 – X2, pero que no debería de ser 1 – (tanh(x))2, quedo en espera de tu amable respuesta. Gracias y Saludos cordiales.

Reply
Rodolfo says:

08/10/2019 at 23:09

Gracias por el aporte de verdad me ha servido para entender más del backpropagation. Aún estoy un poco perdido, entiendo que sólo funciona cuando se tiene 2 entradas y dos salidas? Si uno desea aumentar las entradas y salidas…arrojaría un error en la función fit()…cuál sería la opción para solucionar eso. Gracias nuevamente

Reply
Danny Xie says:

29/10/2019 at 00:24

Hola, tu blog es muy bueno ! Tengo una pregunta ! Al ser tres capas una de entrada con dos neuronas, una oculta con 3 nodos y una de salida on dos nodos, no debería tener 2 sets de pesos? Uno para la capa de entrada a la capa oculta y una para la capa oculta a la capa de salida?

Reply
Luis says:

22/11/2019 at 12:46

Buenos días. He visto en la gráfica de arriba “coste y épocas” que el coste tiende a cero a más épocas. Con más de 14000 epochs, ¿habría overfitting?
Buen blog
Gracias

Reply
Luis says:

22/11/2019 at 14:01

Buenos días. He visto en la gráfica de arriba “coste y épocas” que el coste tiende a cero a más épocas. Con más de 14000 epochs, ¿habría overfitting?
Buen blog
Gracias

Reply
Oscar Noel Amaya Garcia says:

24/01/2020 at 10:10

Hola Ignacio.
En la implementacino de backpropagation de tu algoritmo el delta directamente multiplicando el error por la derivada de la activacion de la capa anterior.

Calculo la diferencia en la capa de salida y el valor obtenido

error = y[i] – a[-1]
deltas = [error * self.activation_prime(a[-1])]

No deberia utilizarse la derivada de la funcion de coste en lugar del coste(error) directamente para obtener el gradiente?

Reply
David says:

09/04/2020 at 17:21

Saludos hermano, ¿este código tiene derechos de autor?. Es posible que le haga algunas modificaciones para darle otra aplicación distinta al carrito arduino.

Gracias y a la espera de tu respuesta

Reply
1. Na8 says:
  
  23/05/2020 at 14:11
  
  Hola David gracias por escribir. Este código está en Github y es de uso libre! Puedes modificarlo y usarlo.
  Si llegas a publicar en algún otro sitio te pediría si puedes enlazar con mi web como referencia.
  Saludos!
  
  Reply
ingae ingae says:

20/04/2020 at 03:30

Hola, cuando cambias la función de activación de tanh a sigmoid, el algoritmo no aprende.

Saludos.

Reply
Angelquiet says:

13/05/2020 at 22:14

Excelente trabajo!!. Una pregunta, ¿se puede realizar este trabajo usando las librerías de keras?

Reply
1. Na8 says:
  
  23/05/2020 at 12:20
  
  Hola Si, claro, sería una red bien sencilla, usando secuencial y una capa! Saludos
  
  Reply
Arturo2000 says:

11/06/2020 at 01:24

Hola, tengo una duda que no consigo entender y me tiene confundido. Para realizar la operación de regresión lineal que realiza cada neurona, tu incluyes una neurona de bias en cada capa menos en la de salida, con lo que se te queda una matriz de pesos de tamaño n neuronas +1 en tu caso 3×4 la primera capa 4×8 la capa intermedia. Dichas matrices las multiplicas con la matriz de datos de entrada y el resultado lo pasas por la activación.

Mi duda es que la función de regresión lineal es matriz de datos de entrada por matriz de pesos sinápticos más bias X×W+bias.

Como es que esta operación es equivalente a la que realizas tu modificando el tamaño de la matriz de pesos sinápticos porqué añades una neurona de bias?

Reply
Arturo2000 says:

11/06/2020 at 01:49

Hola, tengo una duda que no consigo entender y me tiene confundido. Para realizar la operación de regresión lineal que realiza cada neurona, tu incluyes una neurona de bias en cada capa menos en la de salida, con lo que se te queda una matriz de pesos de tamaño n neuronas +1 en tu caso 3×4 la primera capa 4×8 la capa intermedia. Dichas matrices las multiplicas con la matriz de datos de entrada y el resultado lo pasas por la activación.

Mi duda es que la función de regresión lineal es matriz de datos de entrada por matriz de pesos sinápticos más bias X×W+bias.

Como es que esta operación es equivalente a la que realizas tu modificando el tamaño de la matriz de pesos sinápticos porqué añades una neurona de bias?

Reply
Daniel says:

02/09/2020 at 11:52

No tiene un libro sobre cómo crear redes ndneuronales y que matemamatem se necesitan
Mi whats 3316086911

Reply
Lucía says:

21/01/2021 at 20:20

¡Hola! Una vez que la red estuviera lista, ¿cómo podríamos integrarla en una solución como WordPress para poder utilizarla?

He dicho WordPress porque en principio es lo más sencillo a nivel de crear la interfaz, pero no sé si estoy en lo cierto.

¡Muchas gracias!

Reply
Emmanuel says:

28/02/2021 at 00:24

Hola, muy bueno el ejemplo, pero creo que algunas cosas se pueden simplificar.
por ejemplo al decir

def tan(x):
return np.tan(x)

se puede usar la función lambda que python ya trae para crear una función anónima:

tan = lambda x: np.tan(x)

Y se usaría:

tan(0)
0

Esta función fue diseñada para ser simple y rápida, solo ocupa una línea, así que no es para usarse en funciones grandes con otras funciones dentro. Pero la mayor ventaja que tienen es que pueden guardarse en cualquier tipo de variable (arreglos, toupla, diccionarios), con esto último puedes eliminar un par de lineas de código.

Reply
Ricardo says:

06/03/2021 at 19:48

Excelente trabajo, muy practico.. Me costo entender la matriz de pesos, ya que no me había percatado que la bia que utilizas en las capas intermedia es usada como neurona conectada a las neuronas de la capa anterior.

Reply
Ricardo Jose Callejo says:

27/01/2024 at 00:22

El ejemplo este puede usarse con un coche de 2 ruedas? Es el que mencionas en el articulo del Arduino de 4 ruedas o estoy equivocado?

Reply