En este artículo veremos una herramienta muy importante para nuestro kit de Machine Learning y Data Science: PCA para Reducción de dimensiones. Como bonus-track veremos un ejemplo rápido-sencillo en Python usando Scikit-learn.
Introducción a PCA
Imaginemos que queremos predecir los precios de alquiler de vivienda del mercado. Al recopilar información de diversas fuentes tendremos en cuenta variables como tipo de vivienda, tamaño de vivienda, antigüedad, servicios, habitaciones, con/sin jardín, con/sin piscina, con/sin muebles pero también podemos tener en cuenta la distancia al centro, si hay colegio en las cercanías, o supermercados, si es un entorno ruidoso, si tiene autopistas en las cercanías, la “seguridad del barrio”, si se aceptan mascotas, tiene wifi, tiene garaje, trastero… y seguir y seguir sumando variables.
Es posible que cuanta más (y mejor) información, obtengamos una predicción más acertada. Pero también empezaremos a notar que la ejecución de nuestro algoritmo seleccionado (regresión lineal, redes neuronales, etc.) empezará a tomar más y más tiempo y recursos. Es posible que algunas de las variables sean menos importantes y no aporten demasiado valor a la predicción. También podríamos acercarnos peligrosamente a causar overfitting al modelo.
¿No sería mejor tomar menos variables, pero más valiosas?
Al quitar variables estaríamos haciendo Reducción de Dimensiones. Al hacer Reducción de Dimensiones (las características) tendremos menos relaciones entre variables a considerar. Para reducir las dimensiones podemos hacer dos cosas:
- Eliminar por completo dimensiones
- Extracción de Características
Eliminar por completo algunas dimensiones no estaría mal, pero deberemos tener certeza en que estamos quitando dimensiones poco importantes. Por ejemplo para nuestro ejemplo, podemos suponer que el precio de alquiler no cambiará mucho si el dueño acepta mascotas en la vivienda. Podría ser un acierto o podríamos estar perdiendo información importante.
En la Extracción de Características si tenemos 10 características crearemos otras 10 características nuevas independientes en donde cada una de esas “nuevas” características es una combinación de las 10 características “viejas”. Al crear estas nuevas variables independientes lo haremos de una manera específica y las pondremos en un orden de “mejor a peor” sean para predecir a la variable dependiente.
¿Y la reducción de dimensiónes? te preguntarás. Bueno, intentaremos mantener todas las variables posibles, pero prescindiremos de las menos importantes. Como tenemos las variables ordenadas de “mejor a peores predictoras” ya sabemos cuales serán las más y menos valiosas. A diferencia de la eliminación directa de una característica “vieja”, nuestras nuevas variables son combinaciones de todas las variables originales, aunque eliminemos algunas, estaremos manteniendo la información útil de todas las variables iniciales.
¿Qué es Principal Component Analysis?
Entonces Principal Component Analysis es una técnica de Extracción de Características donde combinamos las entradas de una manera específica y podemos eliminar algunas de las variables “menos importantes” manteniendo la parte más importante todas las variables. Como valor añadido, luego de aplicar PCA conseguiremos que todas las nuevas variables sean independientes una de otra.
¿Cómo funciona PCA?
En resumen lo que hace el algoritmo es:
- Estandarizar los datos de entrada (ó Normalización de las Variables)
- Obtener los autovectores y autovalores de la matriz de covarianza
- Ordenar los autovalores de mayor a menor y elegir los “k” autovectores que se correspondan con los autovectores “k” más grandes (donde “k” es el número de dimensiones del nuevo subespacio de características).
- Construir la matriz de proyección W con los “k” autovectores seleccionados.
- Transformamos el dataset original “X estandarizado” vía W para obtener las nuevas características k-dimensionales.
Tranquilos, que todo esto ya lo hace solito scikit-learn (u otros paquetes Python). Ahora que tenemos las nuevas dimensiones, deberemos seleccionar con cuales nos quedamos.
Selección de los Componentes Principales
Típicamente utilizamos PCA para reducir dimensiones del espacio de características original (aunque PCA tiene más aplicaciones). Hemos rankeado las nuevas dimensiones de “mejor a peor reteniendo información”. Pero ¿cuantas elegir para obtener buenas predicciones, sin perder información valiosa? Podemos seguir 3 métodos:
Método 1: Elegimos arbitrariamente “las primeras n dimensiones” (las más importantes). Por ejemplo si lo que queremos es poder graficar en 2 dimensiones, podríamos tomar las 2 características nuevas y usarlas como los ejes X e Y.
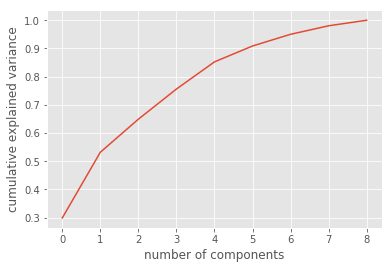
Método 2: calcular la “proporción de variación explicada“ de cada característica e ir tomando dimensiones hasta alcanzar un mínimo que nos propongamos, por ejemplo hasta alcanzar a explicar el 85% de la variabilidad total.
Método 3: Crear una gráfica especial llamada scree plot -a partir del Método 2- y seleccionar cuántas dimensiones usaremos por el método “del codo” en donde identificamos visualmente el punto en donde se produce una caída significativa en la variación explicada relativa a la característica anterior.
¿Pero… porqué funciona PCA?
Suponiendo nuestras características de entrada estandarizadas como la matriz Z y ZT su transpuesta, cuando creamos la matriz de covarianza ZTZ es una matriz que contiene estimados de cómo cada variable de Z se relaciona con cada otra variable de Z. Comprender como una variable es asociada con otra es importante!
Los autovectores representan dirección. Los autovalores representan magnitud. A mayores autovalores, se correlacionan direcciones más importantes.
Por último asumimos que a más variabilidad en una dirección particular se correlaciona con explicar mejor el comportamiento de una variable dependiente. Mucha variabilidad usualmente indica “Información” mientras que poca variabilidad indica “Ruido”.
Ejemplo “mínimo” en Python
Utilizaré un archivo csv de entrada de un ejercicio anterior, en el cual decidíamos si convenía alquilar o comprar casa dadas 9 dimensiones. En este ejemplo:
- normalizamos los datos de entrada,
- aplicamos PCA
- y veremos que con 5 de las nuevas dimensiones (y descartando 4) obtendremos
- hasta un 85% de variación explicada y
- buenas predicciones.
- Realizaremos 2 gráficas:
- una con el acumulado de variabilidad explicada y
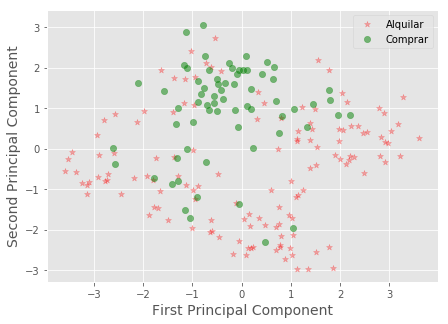
- una gráfica 2D, en donde el eje X e Y serán los 2 primero componentes principales obtenidos por PCA.
Y veremos cómo los resultados “comprar ó alquilar” tienen [icon name=”angle-double-left” class=”” unprefixed_class=””]bastante buena[icon name=”angle-double-right” class=”” unprefixed_class=””] separación en 2 dimensiones.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 |
#importamos librerías import pandas as pd import numpy as np import matplotlib.pyplot as plt %matplotlib inline plt.rcParams['figure.figsize'] = (16, 9) plt.style.use('ggplot') from sklearn.decomposition import PCA from sklearn.preprocessing import StandardScaler #cargamos los datos de entrada dataframe = pd.read_csv(r"comprar_alquilar.csv") print(dataframe.tail(10)) #normalizamos los datos scaler=StandardScaler() df = dataframe.drop(['comprar'], axis=1) # quito la variable dependiente "Y" scaler.fit(df) # calculo la media para poder hacer la transformacion X_scaled=scaler.transform(df)# Ahora si, escalo los datos y los normalizo #Instanciamos objeto PCA y aplicamos pca=PCA(n_components=9) # Otra opción es instanciar pca sólo con dimensiones nuevas hasta obtener un mínimo "explicado" ej.: pca=PCA(.85) pca.fit(X_scaled) # obtener los componentes principales X_pca=pca.transform(X_scaled) # convertimos nuestros datos con las nuevas dimensiones de PCA print("shape of X_pca", X_pca.shape) expl = pca.explained_variance_ratio_ print(expl) print('suma:',sum(expl[0:5])) #Vemos que con 5 componentes tenemos algo mas del 85% de varianza explicada #graficamos el acumulado de varianza explicada en las nuevas dimensiones plt.plot(np.cumsum(pca.explained_variance_ratio_)) plt.xlabel('number of components') plt.ylabel('cumulative explained variance') plt.show() #graficamos en 2 Dimensiones, tomando los 2 primeros componentes principales Xax=X_pca[:,0] Yax=X_pca[:,1] labels=dataframe['comprar'].values cdict={0:'red',1:'green'} labl={0:'Alquilar',1:'Comprar'} marker={0:'*',1:'o'} alpha={0:.3, 1:.5} fig,ax=plt.subplots(figsize=(7,5)) fig.patch.set_facecolor('white') for l in np.unique(labels): ix=np.where(labels==l) ax.scatter(Xax[ix],Yax[ix],c=cdict[l],label=labl[l],s=40,marker=marker[l],alpha=alpha[l]) plt.xlabel("First Principal Component",fontsize=14) plt.ylabel("Second Principal Component",fontsize=14) plt.legend() plt.show() |
Puedes revisar más ejemplos Python en nuestra sección de Práctica
Conclusiones Finales
Con PCA obtenemos:
- una medida de como cada variable se asocia con las otras (matriz de covarianza)
- La dirección en las que nuestros datos están dispersos (autovectores)
- La relativa importancia de esas distintas direcciones (autovalores)
PCA combina nuestros predictores y nos permite deshacernos de los autovectores de menor importancia relativa.
Contras de PCA y variantes
No todo es perfecto en la vida ni en PCA. Como contras, debemos decir que el algoritmo de PCA es muy influenciado por los outliers en los datos. Por esta razón, surgieron variantes de PCA para minimizar esta debilidad. Entre otros se encuentran: RandomizedPCA, SparcePCA y KernelPCA.
Por último decir que PCA fue creado en 1933 y ha surgido una buena alternativa en 2008 llamada t-SNE con un enfoque distinto y del que hablaremos en un futuro artículo…
Te recomiendo leer un nuevo artículo “Interpretación de Modelos de Machine Learning” en donde se comprende mejor la importancia de las diversas features de los modelos.
Resultados de PCA en el mundo real
Para concluir, les comentaré un ejemplo muy interesante que vi para demostrar la eficacia de aplicar PCA. Si conocen el ejercicio “clásico” MNIST (algunos le llaman el Hello Word del Machine Learning), donde tenemos un conjunto de 70.000 imágenes con números “a mano” del 0 al 9 y debemos reconocerlos utilizando alguno de los algoritmos de clasificación.
Pues en el caso de MNIST, nuestras características de entrada son las imágenes de 28×28 pixeles, lo que nos da un total de 748 dimensiones de entrada. Ejecutar Regresión Logística en con una Macbook tarda unos 48 segundos en entrenar el set de datos y lograr una precisión del 91%.
Aplicando PCA al MNIST con una varianza retenida del 90% logramos reducir las dimensiones de 748 a 236. Ejecutar Regresión Logística ahora toma 10 segundos y la precisión obtenida sigue siendo del 91% !!!
Suscripción al Blog
Recibe el próximo artículo quincenal sobre Aprendizaje automático, teoría y ejemplos
Más recursos, seguir leyendo sobre PCA
Mas información en los siguientes enlaces (en inglés):


Hola Juan Ignacio
Nos alegra mucho que tú también estés tratando de enseñar el tema de machine learning en español, ya que son muy pocos los sitios web en este idioma que hablan estos temas.
Me presento, mi nombre es Leonardo Mayorga, soy colombiano, actualmente me encuentro desarrollando un foro de discusión de machine learning, junto con varios compañeros y profesores de la universidad decidimos que sería buena idea dar apertura a un foro de discusión sobre estos temas, te lo presento, este es el foro: https://zonaia.com/
Este foro actualmente se le está agregando guías y tutoriales para que las personas empiecen a aprender machine learning.
Gracias.
Hola Leonardo! Muy bueno el foro, desde aquí animo a todos a visitarlo y aprender sobre redes neuronales
Hola Leonardo, muy buen blog, felicitaciones!
Tengo una duda respecto al query:
Los valores 0 y 1 a que hacen referencia según el ejemplo? Yo tengo un ejercicio pero tiene los valores 2 y 4 en vez de 0 y 1, se puede trabajar con esta información o hay que pasarlo a valores binarios?
Xax=X_pca[:,0]
Yax=X_pca[:,1]
labels=dataframe[‘comprar’].values
cdict={0:’red’,1:’green’}
labl={0:’Alquilar’,1:’Comprar’}
marker={0:’*’,1:’o’}
alpha={0:.3, 1:.5}
Gracias por el apoyo
Hola Juan Ignacio, muy buen blog, felicitaciones!
Tengo una duda respecto al query:
Los valores 0 y 1 a que hacen referencia según el ejemplo? Yo tengo un ejercicio pero tiene los valores 2 y 4 en vez de 0 y 1, se puede trabajar con esta información o hay que pasarlo a valores binarios?
Xax=X_pca[:,0]
Yax=X_pca[:,1]
labels=dataframe[‘comprar’].values
cdict={0:’red’,1:’green’}
labl={0:’Alquilar’,1:’Comprar’}
marker={0:’*’,1:’o’}
alpha={0:.3, 1:.5}
Gracias por el apoyo
Hola Karen, gracias por escribir!
Te comento, en las lineas
Xax=X_pca[:,0]
Yax=X_pca[:,1]
Lo que estoy haciendo es tomar “todos los valores” de las dimensiones 0 y 1 pues son las primeras y -en teoría- las mejores y las uso como variables X e Y para graficar. (También se podrían tomar más dimensiones, según sea conveniente)
Como etiquetas uso 0 => alquilar y 1 => comprar pero podrías usar los valores que a ti te interesen. Realmente se están usando como valores categóricos.
Por ejemplo para ti el valor 2 y 4 podrían significar perros y gatos… depende del problema que estés resolviendo.
Espero haberte ayudado! Saludos
Hola Juan, te quiero agradecer por tu esfuerzo en explicarnos lo relacionado al Machine Learning en español. He estado practicando con tu blog en estos últimos días y he aprendido bastante.
Comprendo que el PCA reduce la dimensión de las variables de entrada; pero ¿cómo puedo saber que variables exactamente son las componentes principales que dan la explicación al modelo?
Tengo ciertas dudas con respecto a la aplicación de la PCA en series temporales multivariadas embedding ¿si la aplico afecta a los valores del mes y el día?
hola, una consulta eso de las 5 dimensiones que representan el 85% de la varianza, son necesariamente los 5 columnas del dataset? (ingresos,gastos comunes,pago_coche,pago_otros y ahorros)
disculpa, recien entiendo que esas columnas son columnas creadas por una combinacion de las variables originales, la cosa es como relacionamos los componentes a las variables originales. sabes como?
Hola Ignacio, lo primero es que muchas gracias por compartir todo este conocimiento. Una pregunta rápida que no veo contestada en el texto de la entrada del Blog.
Indica que son 5 las columnas que llevan el 85% de la varianza explicada, pero ¿Cómo saber a qué características corresponde del dataframe? ¿Es decir, que columnas son las mejores que debo elegir?
Muchas gracias por anticipado.
Hola, gracias por escribir!.
Con PCA no podemos “volver” a las features iniciales porque están “entremezcladas”.
Si quieres evaluar las mejores características debes utilizar otras técnicas. Los modelos de árbol de sklearn tienen un atributo llamado “feature_importance” que te ayuda a elegir las mejores. O tienes algunos algoritmos como “SelectKBest” puedes ver un ejemplo de uso en el artículo de Naive Bayes pero aplica a cualquier modelo.
Saludos!
Buen artículo. Entonces se puede entender que, para este ejemplo, ¿PCA nos sirve sólo para ver si podemos encontrar alguna separación en nuestros datos reduciendo la dimensionalidad?
Si es así, entonces podría probar un clasificador con estas 5 componentes y evaluar. Ahora bien, si el clasificador es bueno y quisiera predecir una nueva instancia, este llegará con los 9 atributos (ingresos, g_comunes, etc.), ¿cómo logro pasar esos nuevos datos a 5 dimensiones nuevamente para probar el clasificador? ¿habría que hacer todo el proceso de nuevo?
Saludos