En este artículo intentaré explicar la teoría relativa a las Redes Neuronales Convolucionales (en inglés CNN) que son el algoritmo utilizado en Aprendizaje Automático para dar la capacidad de “ver” al ordenador. Gracias a esto, desde apenas 1998, podemos clasificar imágenes, detectar diversos tipos de tumores automáticamente, enseñar a conducir a los coches autónomos y un sinfín de otras aplicaciones.
El tema es bastante complejo/complicado e intentaré explicarlo lo más claro posible. En este artículo doy por sentado que tienes conocimientos básicos de cómo funciona una red neuronal artificial multicapa feedforward (fully connected). Si no es así te recomiendo que antes leas sobre ello:
- Historia de las Redes Neuronales, desde el principio hasta 2018
- Breve introducción al DeepLearning con Redes Neuronales
- Crea una sencilla Red Neuronal en Python con Keras y Tensorflow
- Crea una Red Neuronal desde Cero (sin Keras!)
¿Qúe es una CNN? ¿Cómo puede ver una red neuronal? ¿Cómo clasifica imagenes y distingue un perro de un gato?
La CNN es un tipo de Red Neuronal Artificial con aprendizaje supervisado que procesa sus capas imitando al cortex visual del ojo humano para identificar distintas características en las entradas que en definitiva hacen que pueda identificar objetos y “ver”. Para ello, la CNN contiene varias capas ocultas especializadas y con una jerarquía: esto quiere decir que las primeras capas pueden detectar lineas, curvas y se van especializando hasta llegar a capas más profundas que reconocen formas complejas como un rostro o la silueta de un animal.
Necesitaremos…
Recodemos que la red neuronal deberá aprender por sí sola a reconocer una diversidad de objetos dentro de imágenes y para ello necesitaremos una gran cantidad de imágenes -lease más de 10.000 imágenes de gatos, otras 10.000 de perros,…- para que la red pueda captar sus características únicas -de cada objeto- y a su vez, poder generalizarlo -esto es que pueda reconocer como gato tanto a un felino negro, uno blanco, un gato de frente, un gato de perfil, gato saltando, etc.-
Pixeles y neuronas
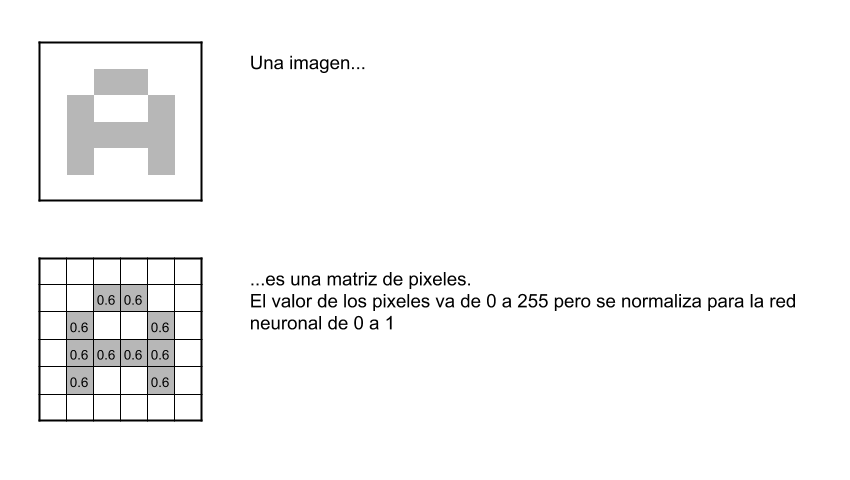
Para comenzar, la red toma como entrada los pixeles de una imagen. Si tenemos una imagen con apenas 28×28 pixeles de alto y ancho, eso equivale a 784 neuronas. Y eso es si sólo tenemos 1 color (escala de grises). Si tuviéramos una imagen a color, necesitaríamos 3 canales (red, green, blue) y entonces usaríamos 28x28x3 = 2352 neuronas de entrada. Esa es nuestra capa de entrada. Para continuar con el ejemplo, supondremos que utilizamos la imagen con 1 sólo color.
No Olvides: Pre-procesamiento
Antes de alimentar la red, recuerda que como entrada nos conviene normalizar los valores. Los colores de los pixeles tienen valores que van de 0 a 255, haremos una transformación de cada pixel: “valor/255” y nos quedará siempre un valor entre 0 y 1.
Convoluciones
Ahora comienza el “procesado distintivo” de las CNN. Es decir, haremos las llamadas “convoluciones”: Estas consisten en tomar “grupos de pixeles cercanos” de la imagen de entrada e ir operando matemáticamente (producto escalar) contra una pequeña matriz que se llama kernel. Ese kernel supongamos de tamaño 3×3 pixels “recorre” todas las neuronas de entrada (de izquierda-derecha, de arriba-abajo) y genera una nueva matriz de salida, que en definitiva será nuestra nueva capa de neuronas ocultas. NOTA: si la imagen fuera a color, el kernel realmente sería de 3x3x3 es decir: un filtro con 3 kernels de 3×3; luego esos 3 filtros se suman (y se le suma una unidad bias) y conformarán 1 salida (cómo si fuera 1 solo canal).
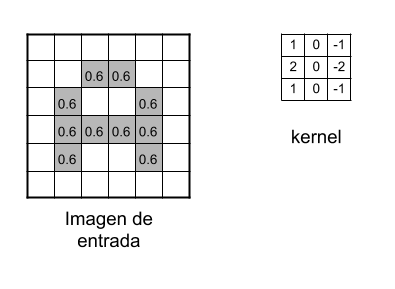
El kernel tomará inicialmente valores aleatorios(1) y se irán ajustando mediante backpropagation. (1)Una mejora es hacer que siga una distribución normal siguiendo simetrías, pero sus valores son aleatorios.
Filtro: conjunto de kernels
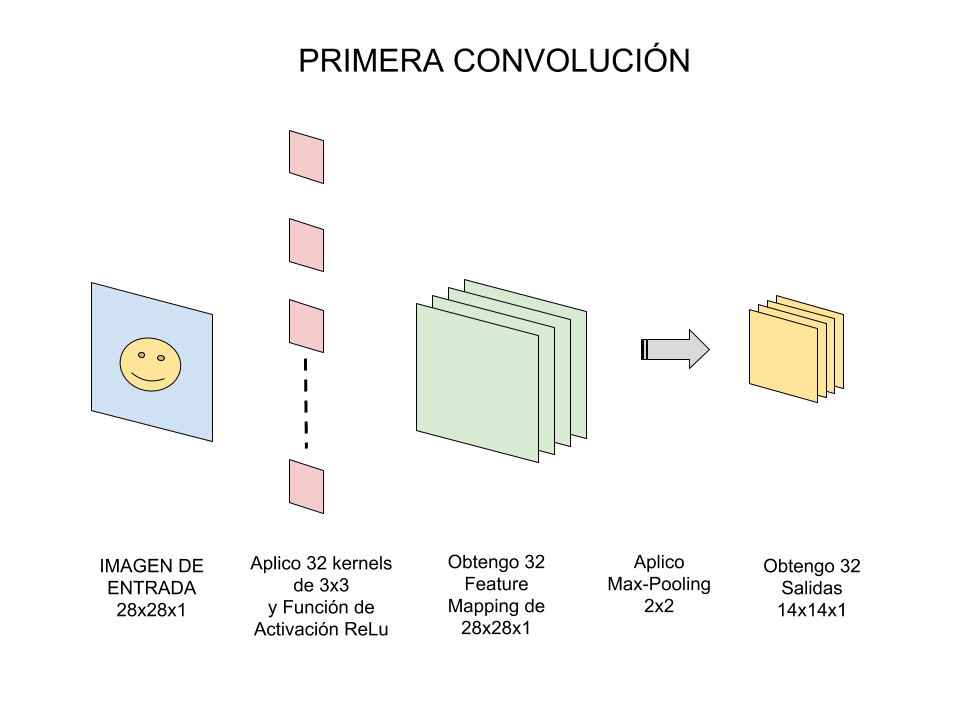
UN DETALLE: en realidad, no aplicaremos 1 sólo kernel, si no que tendremos muchos kernel (su conjunto se llama filtros). Por ejemplo en esta primer convolución podríamos tener 32 filtros, con lo cual realmente obtendremos 32 matrices de salida (este conjunto se conoce como “feature mapping”), cada una de 28x28x1 dando un total del 25.088 neuronas para nuestra PRIMER CAPA OCULTA de neuronas. ¿No les parecen muchas para una imagen cuadrada de apenas 28 pixeles? Imaginen cuántas más serían si tomáramos una imagen de entrada de 224x224x3 (que aún es considerado un tamaño pequeño)…

Aquí vemos al kernel realizando el producto matricial con la imagen de entrada y desplazando de a 1 pixel de izquierda a derecha y de arriba-abajo y va generando una nueva matriz que compone al mapa de features
A medida que vamos desplazando el kernel y vamos obteniendo una “nueva imagen” filtrada por el kernel. En esta primer convolución y siguiendo con el ejemplo anterior, es como si obtuviéramos 32 “imágenes filtradas nuevas”. Estas imágenes nuevas lo que están “dibujando” son ciertas características de la imagen original. Esto ayudará en el futuro a poder distinguir un objeto de otro (por ej. gato ó perro).
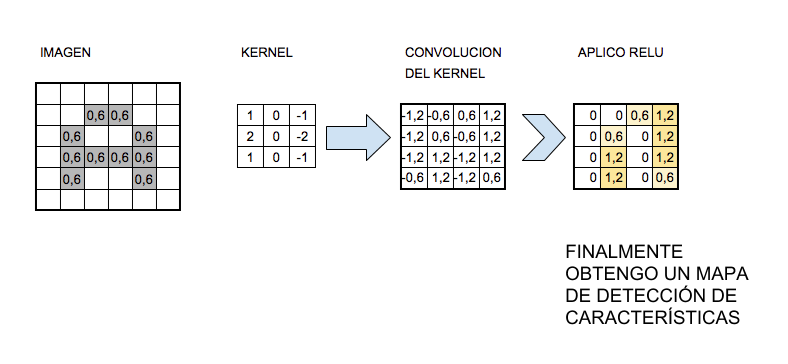
La imagen realiza una convolución con un kernel y aplica la función de activación, en este caso ReLu
La función de Activación
La función de activación más utilizada para este tipo de redes neuronales es la llamada ReLu por Rectifier Linear Unit y consiste en f(x)=max(0,x).
Subsampling
Ahora viene un paso en el que reduciremos la cantidad de neuronas antes de hacer una nueva convolución. ¿Por qué? Como vimos, a partir de nuestra imagen blanco y negro de 28x28px tenemos una primer capa de entrada de 784 neuronas y luego de la primer convolución obtenemos una capa oculta de 25.088 neuronas -que realmente son nuestros 32 mapas de características de 28×28-
Si hiciéramos una nueva convolución a partir de esta capa, el número de neuronas de la próxima capa se iría por las nubes (y ello implica mayor procesamiento)! Para reducir el tamaño de la próxima capa de neuronas haremos un proceso de subsampling en el que reduciremos el tamaño de nuestras imágenes filtradas pero en donde deberán prevalecer las características más importantes que detectó cada filtro. Hay diversos tipos de subsampling, yo comentaré el “más usado”: Max-Pooling
Subsampling con Max-Pooling
Vamos a intentar explicarlo con un ejemplo: supongamos que haremos Max-pooling de tamaño 2×2. Esto quiere decir que recorreremos cada una de nuestras 32 imágenes de características obtenidas anteriormente de 28x28px de izquierda-derecha, arriba-abajo PERO en vez de tomar de a 1 pixel, tomaremos de “2×2” (2 de alto por 2 de ancho = 4 pixeles) e iremos preservando el valor “más alto” de entre esos 4 pixeles (por eso lo de “Max”). En este caso, usando 2×2, la imagen resultante es reducida “a la mitad”y quedará de 14×14 pixeles. Luego de este proceso de subsamplig nos quedarán 32 imágenes de 14×14, pasando de haber tenido 25.088 neuronas a 6272, son bastantes menos y -en teoría- siguen almacenando la información más importante para detectar características deseadas.
¿Ya terminamos? NO: ahora más convoluciones!!
Muy bien, pues esa ha sido una primer convolución: consiste de una entrada, un conjunto de filtros, generamos un mapa de características y hacemos un subsampling. Con lo cual, en el ejemplo de imágenes de 1 sólo color tendremos:
| 1)Entrada: Imagen | 2)Aplico Kernel | 3)Obtengo Feature Mapping | 4)Aplico Max-Pooling | 5)Obtengo “Salida” de la Convolución |
| 28x28x1 | 32 filtros de 3×3 | 28x28x32 | de 2×2 | 14x14x32 |
La primer convolución es capaz de detectar características primitivas como lineas ó curvas. A medida que hagamos más capas con las convoluciones, los mapas de características serán capaces de reconocer formas más complejas, y el conjunto total de capas de convoluciones podrá “ver”.
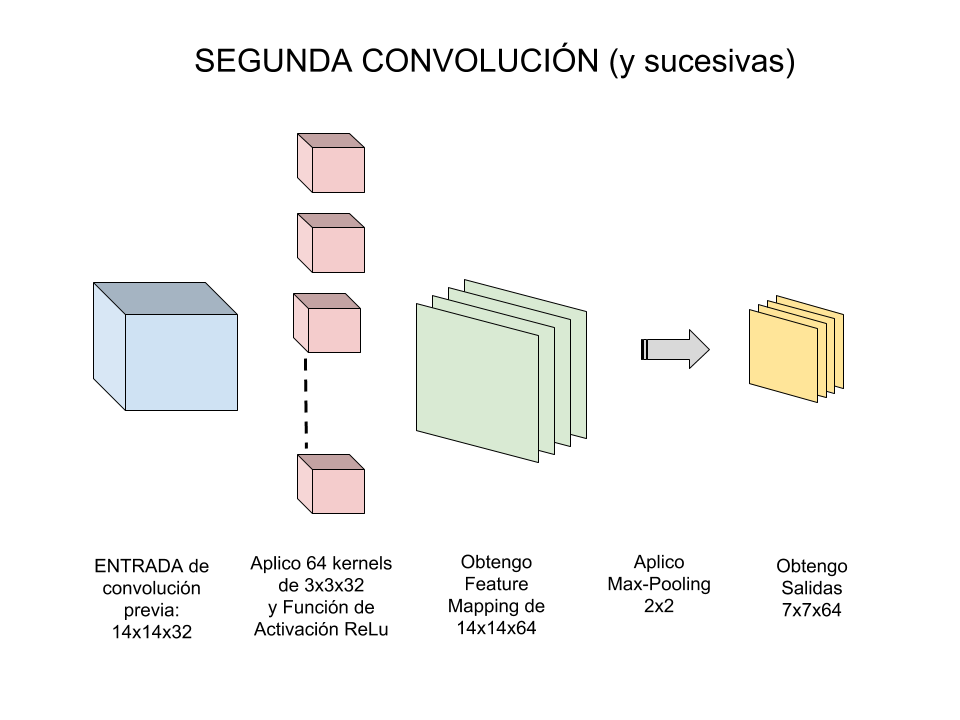
Pues ahora deberemos hacer una Segunda convolución que será:
| 1)Entrada: Imagen | 2)Aplico Kernel | 3)Obtengo Feature Mapping | 4)Aplico Max-Pooling | 5)Obtengo “Salida” de la Convolución |
| 14x14x32 | 64 filtros de 3×3 | 14x14x64 | de 2×2 | 7x7x64 |
La 3er convolución comenzará en tamaño 7×7 pixels y luego del max-pooling quedará en 3×3 con lo cual podríamos hacer sólo 1 convolución más. En este ejemplo empezamos con una imagen de 28x28px e hicimos 3 convoluciones. Si la imagen inicial hubiese sido mayor (de 224x224px) aún hubiéramos podido seguir haciendo convoluciones.
| 1)Entrada: Imagen | 2)Aplico Kernel | 3)Obtengo Feature Mapping | 4)Aplico Max-Pooling | 5)Obtengo “Salida” de la Convolución |
| 7x7x64 | 128 filtros de 3×3 | 7x7x128 | de 2×2 | 3x3x128 |
Llegamos a la última convolución y nos queda el desenlace…
Conectar con una red neuronal “tradicional”.
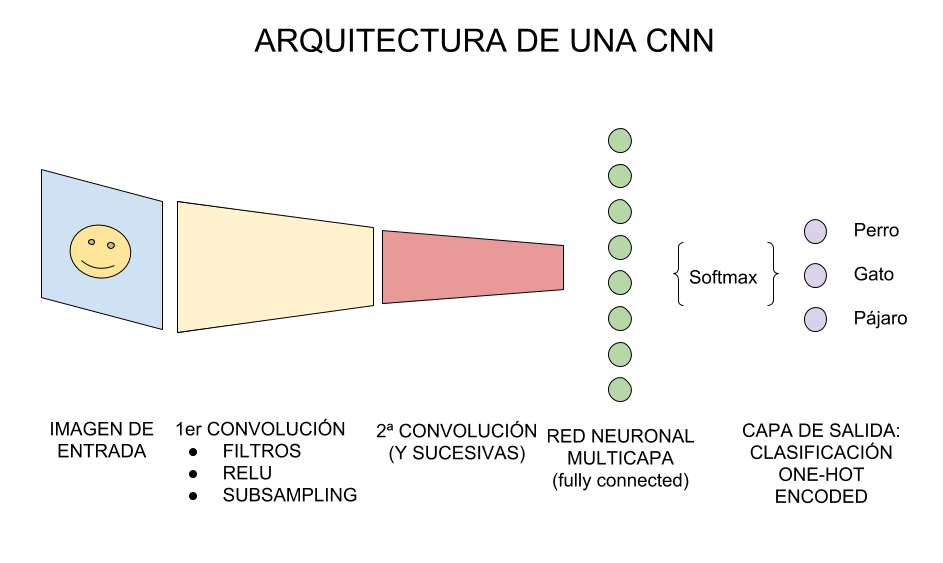
Para terminar, tomaremos la última capa oculta a la que hicimos subsampling, que se dice que es “tridimensional” por tomar la forma -en nuestro ejemplo- 3x3x128 (alto,ancho,mapas) y la “aplanamos”, esto es que deja de ser tridimensional, y pasa a ser una capa de neuronas “tradicionales”, de las que ya conocíamos. Por ejemplo, podríamos aplanar (y conectar) a una nueva capa oculta de 100 neuronas feedforward.
Entonces, a esta nueva capa oculta “tradicional”, le aplicamos una función llamada Softmax que conecta contra la capa de salida final que tendrá la cantidad de neuronas correspondientes con las clases que estamos clasificando. Si clasificamos perros y gatos, serán 2 neuronas. Si es el dataset Mnist numérico serán 10 neuronas de salida. Si clasificamos coches, aviones ó barcos serán 3, etc.
Las salidas al momento del entrenamiento tendrán el formato conocido como “one-hot-encoding” en el que para perros y gatos sera: [1,0] y [0,1], para coches, aviones ó barcos será [1,0,0]; [0,1,0];[0,0,1].
Y la función de Softmax se encarga de pasar a probabilidad (entre 0 y 1) a las neuronas de salida. Por ejemplo una salida [0,2 0,8] nos indica 20% probabilidades de que sea perro y 80% de que sea gato.
¿Y cómo aprendió la CNN a “ver”?: Backpropagation
El proceso es similar al de las redes tradicionales en las que tenemos una entrada y una salida esperada (por eso aprendizaje supervisado) y mediante el backpropagation mejoramos el valor de los pesos de las interconexiones entre capas de neuronas y a medida que iteramos esos pesos se ajustan hasta ser óptimos. PERO…
En el caso de la CNN, deberemos ajustar el valor de los pesos de los distintos kernels. Esto es una gran ventaja al momento del aprendizaje pues como vimos cada kernel es de un tamaño reducido, en nuestro ejemplo en la primer convolución es de tamaño de 3×3, eso son sólo 9 parámetros que debemos ajustar en 32 filtros dan un total de 288 parámetros. En comparación con los pesos entre dos capas de neuronas “tradicionales”: una de 748 y otra de 6272 en donde están TODAS interconectarlas con TODAS y eso equivaldría a tener que entrenar y ajustar más de 4,5 millones de pesos (repito: sólo para 1 capa).
Comparativa entre una red neuronal “tradicional” y una CNN
Dejaré un cuadro resumen para intentar aclarar más las diferencias entre las redes Fully connected y las Convolutional Neural Networks.
| Red “tradicional” Feedforward multicapa | Red Neuronal Convolucional CNN | |
| Datos de entrada en la Capa Inicial | Las características que analizamos. Por ejemplo: ancho, alto, grosor, etc. | Pixeles de una imagen. Si es color, serán 3 capas para rojo,verde,azul |
| Capas ocultas | elegimos una cantidad de neuronas para las capas ocultas. | Tenemos de tipo: * Convolución (con un tamaño de kernel y una cantidad de filtros) * Subsampling |
| Capa de Salida | La cantidad de neuronas que queremos clasificar. Para “comprar” ó “alquilar” serán 2 neuronas. | Debemos “aplanar” la última convolución con una (ó más) capas de neuronas ocultas “tradicionales” y hacer una salida mediante SoftMax a la capa de salida que clasifica “perro” y “gato” serán 2 neuronas. |
| Aprendizaje | Supervisado | Supervisado |
| Interconexiones | Entre capas, todas las neuronas de una capa con la siguiente. | Son muchas menos conexiones necesarias, pues realmente los pesos que ajustamos serán los de los filtros/kernels que usamos. |
| Significado de la cantidad de capas ocultas | Realmente es algo desconocido y no representa algo en sí mismo. | Las capas ocultas son mapas de detección de características de la imagen y tienen jerarquía: primeras capas detectan lineas, luego curvas y formas cada vez más elaboradas. |
| Backpropagation | Se utiliza para ajustar los pesos de todas las interconexiones de las capas | Se utiliza para ajustar los pesos de los kernels. |
Arquitectura básica
Resumiendo: podemos decir que los elementos que usamos para crear CNNs son:
- Entrada: Serán los pixeles de la imagen. Serán alto, ancho y profundidad será 1 sólo color o 3 para Red,Green,Blue.
- Capa De Convolución: procesará la salida de neuronas que están conectadas en “regiones locales” de entrada (es decir pixeles cercanos), calculando el producto escalar entre sus pesos (valor de pixel) y una pequeña región a la que están conectados en el volumen de entrada. Aquí usaremos por ejemplo 32 filtros o la cantidad que decidamos y ese será el volumen de salida.
- “CAPA RELU” aplicará la función de activación en los elementos de la matriz.
- POOL ó SUBSAMPLING: Hará una reducción en las dimensiones alto y ancho, pero se mantiene la profundidad.
- CAPA “TRADICIONAL” red de neuronas feedforward que conectará con la última capa de subsampling y finalizará con la cantidad de neuronas que queremos clasificar.
Finalizando…
Se me quedan en el tintero muchísimas cosas más que explicar… pero creo que lo iré completando con el tiempo o crearé un nuevo artículo con mayor detalle/más técnico. Temas y definiciones como padding, stride, evitar overfitting, image-aumentation, dropout… o por nombrar algunas redes famosas ResNet, AlexNet, GoogLeNet and DenseNet, al mismísimo Yann LeCun… todo eso.. se queda fuera de este texto.
Este artículo pretende ser un punto inicial para seguir investigando y aprendiendo sobre las CNN. Al final dejo enlace a varios artículos para ampliar información sobre CNN.
También puedes pasar a un nuevo nivel y hacer Detección de Objetos en Python!
Conclusiones
Hemos visto cómo este algoritmo utiliza variantes de una red neuronal tradicional y las combina con el comportamiento biológico del ojo humano, para lograr aprender a ver. Recuerda que puedes hacer un ejercicio propuesto para clasificar más de 70.000 imágenes deportivas con Python en tu ordenador!
Suscripción al Blog
Recibe nuevos artículos sobre Machine Learning, redes neuronales y código Python cada 15 días
Más recursos sobre CNN (en Inglés)
- Back Propagation in Convolutional Neural Networks
-
The best explanation of Convolutional Neural Networks on the Internet!
El libro del Blog (en desarrollo)
Puedes colaborar comprando el libro ó lo puedes descargar gratuitamente. Aún está en borrador, pero apreciaré mucho tu ayuda! Contiene Extras descargares como el “Lego Dataset” utilizado en el artículo de Detección de Objetos.


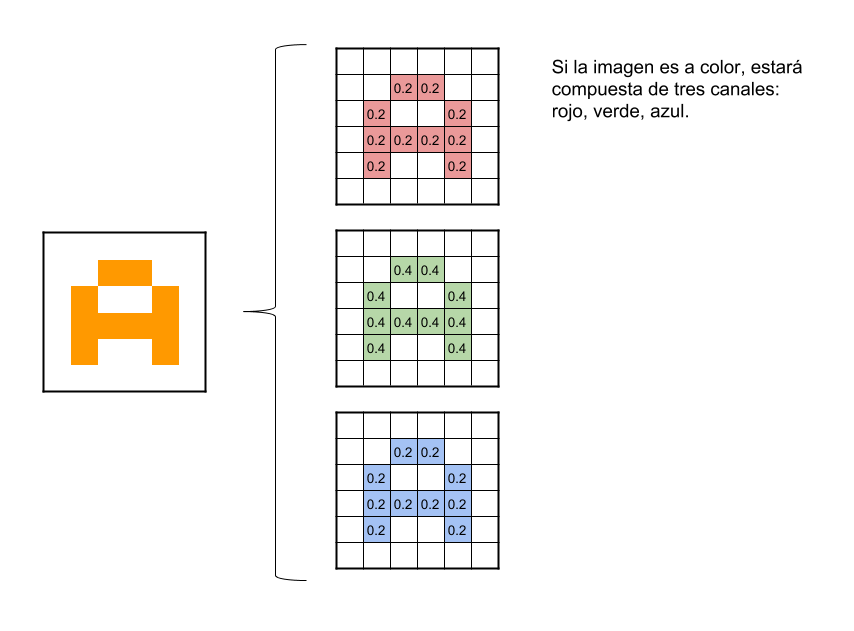

Hola juan buenas noches! Mi nombre es Joaquin y estudio ing Industrial en Rosario. La verdad que me empezo a interesar mucho el machine learning y en especial el deep learning. Gracias a tu guia de aprendizaje estoy metiendome mas con esto. Actualmente trabajo en un empresa siderurgica donde uno de los productos que fabrica son clavos. Te quería consultar si se puede clasificar imagenes ( en este caso clavos defectuosos de clavos buenos) mediante estas redes convolucionales. Me gustaria poder contactarte por mail y explicarte bien el proceso.
La verdad te felicito por todo el aporte que brindas. Lo explicas excelente.
Un abrazo!!!
Hola Joaquin, gracias por escribir. Sí que se puede hacer ese tipo de clasificaciones, habría que generar un BUEN dataset con los diversos ejemplos de clavos “buenos” y defectuosos para que la red (CNN) pueda aprender correctamente. Puedes escribirme en el formulario de la página de contacto ó al email que es info (at) aprendemachinelearning.com
Saludos!
Hola Juan! Soy Victor, soy ingeniero informático y estoy empezando a meter un poco el morro en el mundo de Machine Learning, Deep Learning e IA en general. Desde que empecé a documentarme, tu página me ayudó mucho :).
Estoy haciendo una CNN que aprenda a distinguir entre perros y gatos (la práctica común), tengo un dataset de 1500 imágenes de perros y otras 1500 de gatos, al intentar darle forma a la CNN se me presentan diversas dudas:
– ¿Cómo determino cual es el tamaño del kernel para la capa de convolución? En tu ejemplo, la primera capa de convolución tiene un tamaño de 3×3 con 32 kernels para una imagen de 28×28 con un solo canal. Mis imagenes son de 250x250x3 (ya que es RGB). He estado pensando en reducir el canal de cada imagen del dataset convirtiendo la imagen a escala de grises, y cuando quiera analizar imágenes nuevas, hacer el mismo proceso.
Tambien me pregunto… ¿Cuantas capas de Convolucion+Pooling son las adecuadas?
De momento mi algoritmo tiene una única capa de convolución de 20×20 con 10 kernels. y un pooling usando Max-Pooling de 2×2 con un Stride de 2. A la hora de hacer el entrenamiento, no veo evolución y es como si no hiciese nada, como si entrenar una imagen tardare 10 minutos.
¿Hay alguna manera de determinar una correcta parametrización?
¡¡Muchas gracias!!
Hola Victor, gracias por escribir, te intento responder:
– si puedes usar imágenes más grandes de 28×28 mejor, pero recuerda que tardará más en entrenar. Podrías probar con el doble, por ejemplo imágenes de 56×56.
– como tamaño de kernel no se suele usar de más de 5×5.
– las cantidades se suelen usar 64, 32, 16, 8 y de hecho, se usan de más a menos.
– Yo que tu, mantendría los 3 canales RGB pues ayudará a que detecte mejor la CNN.
-Sobre la cantidad de capas, hay que intentar siempre “la mínima cantidad” por ejemplo, pruebas con 2 ó 3 y ver que resultado obtienes. Si es malo iría sumando de a 1 capa.
-imagino que le toma 10 minutos por tomar imagenes en tamaño completo. Intenta disminuir el tamaño, eso le afecta mucho.
– Minimo intenta usar 2 capas, recuerda que si usas 1 sólo, la CNN “solo podrá distinguir formas básicas” y como un perro o un gato son más complejos que formas básicas…
– Prueba sin hacer el Stride.
-Determinar una correcta parametrización es muy difícil, es hacer un equilibrio entre todo, incluyendo CPU y RAM…
Como último consejo, puedes mirar el curso de fast.ai que ademas en su librería implementa varias utilidades para redes CNN que te pueden ser de gran ayuda
Saludos!
holaaa… podrias hacer un artículo sobre Dense Net … me ayudaría mucho en un trabajo
por cierto muuuuy bueno tu blog .. me ha servido muchisimo
Hola Lukas, gracias por escribir. Lo tendré en cuenta, a ver si pronto puedo sacar un artículo con esa temática. Saludos!
Gracias por esto !!. Muy claro.
Hola Juan, me ha encantado tu blog, me ha ayudado a entender muchos conceptos. Aún tengo algunas dudas, no se si puedas orientarme un poco. Estoy trabajando en una CNN de object detection, para detectar productos en anaqueles de supermercados, en algunas pruebas que he hecho, he etiquetado manualmente cada producto en fotos (2000×2000) de anaqueles completas, y ha funcionando muy bien, hemos etiquetado cerca de 300 fotos, con 20 clases, cada clase ha sido el código de barras de un producto.
Pero tengo ciertas dudas.
Cuando yo creo un dataset de imagenes individuales de los productos, (100 x 100), y le paso despues una foto de 2000×2000 donde vienen varios productos, no me detecta nada. =() Esto es normal ?
Es decir debe existir una relación entre los tamaños de las imagenes entrenadas y las imagenes que se van a procesar ???
Otra opción que estoy explorando es, crear anaqueles virtuales con imagenes de productos, aplicando ImageDataGenerator de keras,
para usar estas fotos procesadas para entrenar mi modelo. Crees que eso sea posible ?
Nuevamente muchas gracias por el tiempo que has dedicado a este blog
Hola! Excelente tu explicación!!
Tengo una duda, estoy siguiendo la red del ejemplo paso a paso y, como la estoy pensando yo, no coinciden los tamaños. Podrías decirme dónde me estoy equivocando? Tal vez no comprendí el max pooling..
Porque a mí me parece que se redujo el tamaño en 1/4(por el ejemplo de max pooling) entonces en la primer convolución de 28x28x1 (o 26x26x1) pasaría a 7x7x1
Gracias por este blog!!
Saludos
Porque aplicó otra vez la convolución.
En la primera convolución paso de 28x28x# a 14x14x#
En la segunda convolución paso de 14x14x# a 7x7x#
Hola, muchísimas gracias por tu blog, me encanta.
Estoy empezando con IA y ML y ahora estoy adentrándome en DL, pero tengo una duda.
En tu artículo, y en muchos otros en la web, se habla de 32 filtros en la primera capa convolucional de los ejemplos.
Por favor, podrías explicarme por qué 32 y no otro número?
Mil gracias de antemano,
Jerónimo
Por Convención veras que se usan potencias de 2, pero realmente se pueden modificar y verás otras arquitecturas con diversos valores.
Saludos y gracias por escribir!
Muchas gracias a tí, las publicaciones que realizas son fantásticas. Estoy estudiando un máster en IA y algún artículo tuyo me ha sido de ayuda indudable para aclarar conceptos.
Hola de nuevo Juan, he tenido unos días complicados y hasta ahora no he podidop terminar de leer el post.
Me surge una pregunta,….¿cómo se determina el numero adecuado de capas (convolucional + pooling) que debería contener la red?
Gracias de antemano
por cierto intenté comprar tu libro y creo que el banco bloqueaba la operacion, ¿cuándo lo tendrás en amazon?
No entiendo muy bien como funciona la segunda capa convolucional. Tiene como entrada 32 matrices de dimensión 14×14 y la capa tiene 64 kernels. No habría que realizar 64 convoluciones a cada una de las 32 matrices de entradas teniendo 64*32 salidas?
Me queda la misma duda, ojalá nos ayuden a aclararla.
Solamente para felicitarte, increíble explicación, aprendí más en esto que en un video de 1 hora
Jajaja, muchas gracias! Me alegra saberlo!
En el contexto de una CNN para procesar texto natural de comentarios de usuarios y determinar si corresponde a una de 7 posibles emociones, ¿qué impacto podría tener achicar demasiado (menos de 4) ese tamaño de filtro?
Buen tutorial, pero hay una cosas que no entiendo en el ejemplo pones que partes de una entrada de 28×281 y le aplicas unos filtros de 3x3x32 entonces la matrices de caracteristicas no deberian de ser 26x26x32 y no 28x28x32 como pones?
Hola Miguel, está bien lo que apuntas y a eso se le llama “Border Effect Problem”, sin embargo para resolverlo se usa el Padding. Te dejo un enlace muy interesante donde se explica todo esto:
Padding and Stride for CNN
Saludos!
Hola Juan Ignacio!! Magnífico artículo. Muchas gracias!
Una pregunta. Esa primer capa oculta «de convolución» aplica 32 filtros, por lo que generamos 32 matrices de salida.
Si a continuación aplicamos «dropout»… ¿esto implica que ignoramos o desconectamos algunas de esas matrices?
En un MLP me puedo imaginar desconectar algunas neuronas, pero en una CNN no.
Bueno eso es todo. Disculpas si la pregunta es trivial.
Un saludo desde Mendoza, Argentina. Abrazo!!
Hola Wilfredo, gracias por escribir, lo que hace el dropout es anular algunas de las neuronas de una capa de la CNN “a propósito”, para forzar al resto a reacomodar sus pesos para que a pesar de esa falta de información, sea capaz de reconocer el patrón que se busca.
Cuando aprendí esto, me quedé perplejo y fascinado a la vez!.
Si te pones a pensar, imagino que miras un objeto tapándote los ojos con las manos, pero dejando un poquito de espacio entre los dedos (como si fuera una persiana). A pesar de estar “tapando” un poco tu visión, seguro serás capaz de interpretar la imagen que ves.
Un Saludo!
Hola Juan Ignacio!
Muchas Gracias por tu respuesta!!
Ahora me puedo dar una mejor idea de la aplicación de “Dropout” en CNN.
Lo que todavía no entiendo muy bien qué pasa con la actualización de los “pesos” de esas neuronas desconectadas, en cada iteración.
En las CNN todas las neuronas de un “mapa de características” comparten los mismos pesos… (ojo creo que es así…!). Ahí está lo que no entiendo.
Buscando en el manual de Keras, existe una variación del método “Dropout” que se llama “SpatialDropout2D”, que pone a cero todo un mapa de características, en vez de poner a cero elementos individuales de esos arrays.
https://keras.io/api/layers/regularization_layers/spatial_dropout2d/
Bueno Juan Ignacio, eso es todo. Espero haber podido expresar bien mis dudas.
Abrazo, y Felicitaciones por tu trabajo!
…También encontré un lindo artículo sobre la diferencia que existe al aplicar “Dropout” a capas densamente conectadas y a capas convolucionales:
https://towardsdatascience.com/dropout-on-convolutional-layers-is-weird-5c6ab14f19b2
El autor de esta nota, Jacob Reinhold, dice que la operación de Dropout sobre capas convolucionales es “extraña”. También he visto que muchos autores aconsejan “no aplicar” Dropout en capas convolucionales. En fin… todo muy apasionante!
Muchas gracias!
Gracias por el artículo, una pregunta como es la entrada de la segunda capa en la que aplico 64 filtros? Según entiendo esa entrada ya tiene 32 de profundidad (salida primera capa), pero parece que de alguna forma se vuelve de profundidad 1 y se repite el proceso pero ahora con profundidad 64. Me ayudas a entender eso?
Hola! Se puede utilizar para imágenes que no son cuadradas? Gracias
Si, claro!, eso lo defines tu, que eres el data engineer 🙂
Saludos